Elastizitätsmodul

Spannungs-Dehnungs-Linie gemäß DIN EN 1992-1-1 für die Schnittgrößenermittlung mit nichtlinearen Verfahren und für Verformungsberechnungen mit:
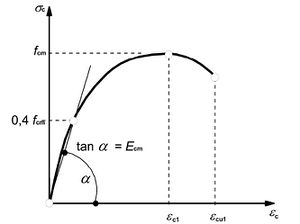
f_cm: Mittelwert der Zylinderdruckfestigkeit des Betons
E_cm: mittlerer Elastizitätsmodul als Sekante
ε_c1: Dehnung des Betons unter der Maximalspannung f_c (einaxiale Betondruckfestigkeit)
ε_cu1: rechnerische Bruchdehnung des Betons

Der Elastizitätsmodul oder auch E-Modul ist der Materialkennwert für das elastische Verformungsverhalten eines durch Druck oder Zug beanspruchten Werkstoffs und wird in N/mm² angegeben. Der Elastizitätsmodul gibt das Verhältnis der Spannung zur zugehörigen elastischen Verformung an. Er ist also definiert durch das Verhältnis zwischen einwirkender Spannung und resultierender Längenänderung (Dehnung) innerhalb eines Lastbereichs, in dem sich Spannungen und Verformungen noch proportional zueinander verhalten. Der Elastizitätsmodul von Beton hat im Rahmen der Nachweise bei behinderter Verformung und bei Verformungsnachweisen wie z. B. der Durchbiegung einen erheblichen Einfluss.
Physikalisch wird das elastische Verhalten eines homogenen Materials von der Bindungskraft zwischen den Atomen und dem Atomabstand bestimmt. Je stärker diese Bindungskraft ist, umso steiler verläuft die Spannungs-Dehnungs-Linie im Bereich des Nulldurchgangs und umso höher ist der Elastizitätsmodul des Materials.
Beton ist aber kein homogener Baustoff, sondern muss hinsichtlich des Elastizitätsmoduls näherungsweise als Zweistoffsystem (Zementstein und Gesteinskörnung) angesehen werden. Der Elastizitätsmodul von Beton hängt von den Elastizitätsmodulen dieser beiden Stoffe ab. Näherungsweise wird der Elastizitätsmodul als Sekantenmodul der Spannungs-Dehnungs-Linie im elastischen Bereich aufgefasst. Der Sekantenmodul gibt die Steigung der Spannungs-Dehnungs-Linie zwischen dem Ursprung in σ_c = 0 bis zu 40 % des Mittelwerts der Betondruckfestigkeit f_cm an. Der Sekantenmodul entspricht näherungsweise dem in der Baustoffprüfung bestimmten Elastizitätsmodul. Das Sekantenmodul wird für Verformungsberechnungen angesetzt.
Der Elastizitätsmodul von Normalbeton liegt mit 25800 N/mm² für einen Beton C 12/15 bis 45200 N/mm² für einen Beton C 100/115 im Alter von 28 d (Tabellenwerte aus DIN EN 1992-1-1 für quarzithaltige Gesteinskörnungen) zwischen dem Elastizitätsmodul der Zementstein-Matrix mit 5000 bis 20000 N/mm² und dem Elastizitätsmodul der Gesteinskörnung mit 10000 bis 100000 N/mm².

Rechenwerte des Elastizitätsmoduls
Insgesamt besteht ein enger Zusammenhang zwischen Betondruckfestigkeit und Elastizitätsmodul, der daher in der Regel für statische Berechnungen aus der Druckfestigkeit des Betons abgeleitet wird. DIN EN 1992-1-1 stellt dafür folgende analytische Beziehung auf:
E_cm = 22×(f_cm/10)^0,3
mit E_cm = mitteler Elastizitätsmodul als Sekante und f_cm = Mittelwert der Zylinderdruckfestigkeit des Betons
Tabelle 3.1 in DIN EN 1992-1-1 ordnet den einzelen Druckfestigkeitsklassen C12/15 bis C90/105 entsprechende Werte für den Elastizitätsmodul zu. Die Verwendung dieser Werte kann aber zu einer Über- bzw. Unterschätzung dieses Bemessungswerts führen.
Genauere Werte liefert die experimentelle Bestimmung des Elastizitätsmoduls mithilfe einer annähernd zerstörungsfreien einaxialen Druckprüfung. Dabei wird der Probekörper bis zu einem Drittel der Betondruckfestigkeit, die zuvor an anderen Probekörpern ermittelt worden sein muss, belastet. Bei der Laststeigerung werden die Last und die entsprechende Verformung aufgezeichnet. Damit der Einfluss der viskosen und verzögert elastischen Verformung gering bleibt, wird der Probekörper zyklisch belastet. Aus der sich daraus ergebenden Spannungs-Dehnungs-Linie wird dann der statische Elastizitätsmodul bestimmt. Gemäß DIN EN 12390-13 sind zwei Prüfverfahren (Verfahren A und B) möglich, wobei Verfahren B die Bestimmung in Analogie zur vorherigen Prüfnorm DIN 1048-5 ermöglicht.
Die Bestimmung des dynamischen Elastizitätsmoduls erfolgt z. B. über Resonanzfrequenzmessungen mit einem Ultraschall-Messgerät.
Das Verhältnis von dynamischem zu statischem Elastizitätsmodul ist nicht konstant, sondern vom Porenraum des Zementsteins abhängig.

Siehe auch:

• Verformung
• Formänderungen

Literatur

• Manns, Wilhelm: Elastizitätsmodul von Zementstein und Beton. In: beton 9-1970, S. 401, und beton 10-1970, S. 455
• Brameshuber, Wolfgang; Brockmann, Tanja: Ringversuch zur Ermittlung des statischen Elastizitätsmoduls von Beton. In: beton 6-2003, S. 295
• Scheydt, Jennifer C.; Breit, Wolfgang; Schäffel, Patrick: Bestimmung des E-Moduls von Beton – Vergleich von DIN EN 12390-13 und DIN 1048-5. beton 4-2015, Seite 132f
• Brameshuber, Wolfgang: Elastizitätsmodul von Beton. In: beton 11-2016, S. 442
• Heiermann, Thomas; Raupach, Michael: Elastizitätsmodul von Beton. In: beton 1+2/2018, S. 10