Fuller-Kurve: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
[[Datei:Fullerkurve.jpg|mini|Fullerkurve für die „ideale“ Kornzusammensetzung eines Korngemischs 0/32]] | |||
Fuller-Parabel; Fuller-Gleichung<br /> | |||
Die amerikanischen Ingenieure [[Fuller, William Barnard|William B. Fuller]] und [[Thompson, Sanford Eleazer|Sanford E. Thompson]] waren 1907 die ersten, deren systematische Versuche über eine zweckmäßige [[Kornzusammensetzung]] ([[Idealsieblinie]]) zum Erfolg führten. Sie entwickelten die sogenannten Fuller-Kurve, die sich nach der (Fuller-)Gleichung auftragen lässt:<br /> | Die amerikanischen Ingenieure [[Fuller, William Barnard|William B. Fuller]] und [[Thompson, Sanford Eleazer|Sanford E. Thompson]] waren 1907 die ersten, deren systematische Versuche über eine zweckmäßige [[Kornzusammensetzung]] ([[Idealsieblinie]]) zum Erfolg führten. Sie entwickelten die sogenannten Fuller-Kurve, die sich nach der (Fuller-)Gleichung auftragen lässt:<br /> | ||
A = 100 x | A = 100 x (d/D)<sup>n</sup><br /> | ||
mit:<br>A = [[Siebdurchgang]] | mit:<br> | ||
d = Sieböffnung<br /> | A = [[Siebdurchgang]] in M.-% einschl. Zement, der durch das Sieb mit der Nennweite d hindurchgeht<br /> | ||
D = [[Größtkorn]]<br /> | d = Korndurchmesser (= Sieböffnung) zwischen 0 und D, für den der prozentuale Anteil im Korngemisch berechnet werden soll<br /> | ||
D = Durchmesser des [[Größtkorn|Größtkorns]] der zu berechnenden [[Sieblinie]]<br /> | |||
Eugen Dyckerhoff hatte | n = Exponent zur Berücksichtigung der [[Kornform]]<br /> | ||
Fuller und Thompson gingen von einer idealen Kugel als [[Kornform]] aus. Der entsprechende Exponent n für diese Kornform ist 0,5. Eine optimale Packungsdichte wird aber für Kiessand bei etwa n = 0,4 und für gebrochenen Naturstein bei etwa n = | |||
0,3 erreicht. Für diese Werte aufgetragene Fuller-Kurven zeigen, dass die Gesteinskörnung umso feiner sein muss, je mehr die [[Kornform]] von der Kugelform abweicht, aufgrund der größeren Oberfläche verbunden mit einem höheren Zementleimbedarf.<br /> | |||
Die Fuller-Kurve bezieht sich nicht nur auf die [[Gesteinskörnung]], sondern schließt den [[Zement]] mit ein. Durch Modifikation, so dass der Zement unberücksichtigt bleibt, wurden die heute gültigen [[Regelsieblinie]]n entwickelt.<br /> | |||
Eugen Dyckerhoff hatte schon 1868 auf die Zusammenhänge zwischen Packungsdichte, Zementleimbedarf und Druckfestigkeit hingewiesen, wurde jedoch kaum beachtet. | |||
==Literatur== | ==Literatur== | ||
* Fuller, W.B.; Thompson S.E.: The laws of proportioning concrete. Transactions of the American Society of Civil Engineers 33 (1907):222–298 | * Fuller, W.B.; Thompson S.E.: The laws of proportioning concrete. Transactions of the American Society of Civil Engineers 33 (1907):222–298 | ||
* Weber, Robert; Riechers, Hans-Joachim: Kies und Sand für Beton. Verlag Bau+Technik GmbH, Düsseldorf 2003 | |||
* Stark, Jochen; Wicht, Bernd: Geschichte der Baustoffe. Springer-Verlag, 2013 | * Stark, Jochen; Wicht, Bernd: Geschichte der Baustoffe. Springer-Verlag, 2013 | ||
[[Category: Gesteinskörnung]] | [[Category: Gesteinskörnung]] | ||
Version vom 1. April 2016, 08:25 Uhr
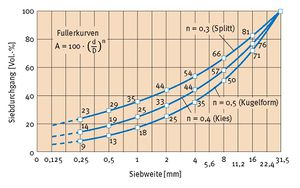
Fuller-Parabel; Fuller-Gleichung
Die amerikanischen Ingenieure William B. Fuller und Sanford E. Thompson waren 1907 die ersten, deren systematische Versuche über eine zweckmäßige Kornzusammensetzung (Idealsieblinie) zum Erfolg führten. Sie entwickelten die sogenannten Fuller-Kurve, die sich nach der (Fuller-)Gleichung auftragen lässt:
A = 100 x (d/D)n
mit:
A = Siebdurchgang in M.-% einschl. Zement, der durch das Sieb mit der Nennweite d hindurchgeht
d = Korndurchmesser (= Sieböffnung) zwischen 0 und D, für den der prozentuale Anteil im Korngemisch berechnet werden soll
D = Durchmesser des Größtkorns der zu berechnenden Sieblinie
n = Exponent zur Berücksichtigung der Kornform
Fuller und Thompson gingen von einer idealen Kugel als Kornform aus. Der entsprechende Exponent n für diese Kornform ist 0,5. Eine optimale Packungsdichte wird aber für Kiessand bei etwa n = 0,4 und für gebrochenen Naturstein bei etwa n =
0,3 erreicht. Für diese Werte aufgetragene Fuller-Kurven zeigen, dass die Gesteinskörnung umso feiner sein muss, je mehr die Kornform von der Kugelform abweicht, aufgrund der größeren Oberfläche verbunden mit einem höheren Zementleimbedarf.
Die Fuller-Kurve bezieht sich nicht nur auf die Gesteinskörnung, sondern schließt den Zement mit ein. Durch Modifikation, so dass der Zement unberücksichtigt bleibt, wurden die heute gültigen Regelsieblinien entwickelt.
Eugen Dyckerhoff hatte schon 1868 auf die Zusammenhänge zwischen Packungsdichte, Zementleimbedarf und Druckfestigkeit hingewiesen, wurde jedoch kaum beachtet.
Literatur
- Fuller, W.B.; Thompson S.E.: The laws of proportioning concrete. Transactions of the American Society of Civil Engineers 33 (1907):222–298
- Weber, Robert; Riechers, Hans-Joachim: Kies und Sand für Beton. Verlag Bau+Technik GmbH, Düsseldorf 2003
- Stark, Jochen; Wicht, Bernd: Geschichte der Baustoffe. Springer-Verlag, 2013
