Dauerschwingfestigkeit: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (Eine dazwischenliegende Version desselben Benutzers wird nicht angezeigt) | |||
| Zeile 5: | Zeile 5: | ||
* Dauerschwellfestigkeit: von Null auf einen Höchstwert ständig wechselnde Belastung | * Dauerschwellfestigkeit: von Null auf einen Höchstwert ständig wechselnde Belastung | ||
* Dauerschwingfestigkeit: um einen Mittelwert schwingende Lastwechsel zwischen Ober- und Unterlast unter Druckbelastung | * Dauerschwingfestigkeit: um einen Mittelwert schwingende Lastwechsel zwischen Ober- und Unterlast unter Druckbelastung | ||
Die Dauerschwingfestigkeit | Die Dauerschwingfestigkeit bezeichnet das Verformungs- und Versagensverhalten von Werkstoffen bei dynamischer/zyklischer Beanspruchung, wie sie zum Beispiel bei [[Brückenbau|Brücken]] häufig auftritt.<br /> | ||
Die bei häufig wiederholten wechselnden Lasten ertragbare Beanspruchung des Betons, die Dauerschwingfestigkeit, wird bei Bedarf in typisierten Druckschwellversuchen (Wöhlerversuch) mit konstanter Schwingbreite ermittelt. Auf die Kurzzeitfestigkeit bezogen ist sie weitgehend unabhängig von [[Betonzusammensetzung]] und [[Druckfestigkeitsklassen|Druckfestigkeitsklasse]].<br /> | Die bei häufig wiederholten wechselnden Lasten ertragbare Beanspruchung des Betons, die Dauerschwingfestigkeit, wird bei Bedarf in typisierten Druckschwellversuchen (Wöhlerversuch) mit konstanter Schwingbreite ermittelt. Auf die Kurzzeitfestigkeit bezogen ist sie weitgehend unabhängig von [[Betonzusammensetzung]] und [[Druckfestigkeitsklassen|Druckfestigkeitsklasse]].<br /> | ||
Die Ergebnisse des Wöhlerversuchs bilden in einem Diagramm mit den Ordinaten Schwingbeanspruchung und Lastspielzahl eingetragen eine Wöhlerkurve bzw. Wöhlerlinie. Sie gibt die Anzahl der Lastwechsel bis zum "Versagen" (= Eintreten von [[Risse|Rissen]] oder Brüchen) wieder. Der Eisenbahningenieur August Wöhler (1819 - 1914) stellte nach vermehrt auftretendem Brüchen an Radsatzwellen, die der statischen Belastung eigentlich hätten standhalten müssen, fest, dass schwingende Belastungen ein Bauteil mehr beanspruchen als statische. | Die Ergebnisse des Wöhlerversuchs bilden in einem Diagramm mit den Ordinaten Schwingbeanspruchung und Lastspielzahl eingetragen eine Wöhlerkurve bzw. Wöhlerlinie. Sie gibt die Anzahl der Lastwechsel bis zum "Versagen" (= Eintreten von [[Risse|Rissen]] oder Brüchen) wieder. Der Eisenbahningenieur August Wöhler (1819 - 1914) stellte nach vermehrt auftretendem Brüchen an Radsatzwellen, die der statischen Belastung eigentlich hätten standhalten müssen, fest, dass schwingende Belastungen ein Bauteil mehr beanspruchen als statische. | ||
Aktuelle Version vom 15. April 2020, 10:22 Uhr
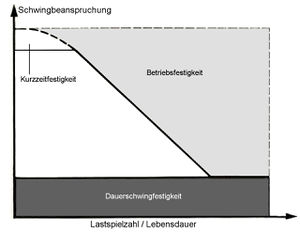
In Abhängigkeit von der zeitlichen Entwicklung der Belastung werden bei der Druckfestigkeit von Beton unterschieden:
- Kurzzeitfestigkeit: einmalige kurzzeitige Belastung
- Dauerstandfestigkeit: dauernde konstante Belastung
- Dauerschwellfestigkeit: von Null auf einen Höchstwert ständig wechselnde Belastung
- Dauerschwingfestigkeit: um einen Mittelwert schwingende Lastwechsel zwischen Ober- und Unterlast unter Druckbelastung
Die Dauerschwingfestigkeit bezeichnet das Verformungs- und Versagensverhalten von Werkstoffen bei dynamischer/zyklischer Beanspruchung, wie sie zum Beispiel bei Brücken häufig auftritt.
Die bei häufig wiederholten wechselnden Lasten ertragbare Beanspruchung des Betons, die Dauerschwingfestigkeit, wird bei Bedarf in typisierten Druckschwellversuchen (Wöhlerversuch) mit konstanter Schwingbreite ermittelt. Auf die Kurzzeitfestigkeit bezogen ist sie weitgehend unabhängig von Betonzusammensetzung und Druckfestigkeitsklasse.
Die Ergebnisse des Wöhlerversuchs bilden in einem Diagramm mit den Ordinaten Schwingbeanspruchung und Lastspielzahl eingetragen eine Wöhlerkurve bzw. Wöhlerlinie. Sie gibt die Anzahl der Lastwechsel bis zum "Versagen" (= Eintreten von Rissen oder Brüchen) wieder. Der Eisenbahningenieur August Wöhler (1819 - 1914) stellte nach vermehrt auftretendem Brüchen an Radsatzwellen, die der statischen Belastung eigentlich hätten standhalten müssen, fest, dass schwingende Belastungen ein Bauteil mehr beanspruchen als statische.
Literatur
- Weigler, Helmut: Beton bei häufig wiederholter Beanspruchung. beton 5/1981, S. 189 f
- Rinder, Tassilo; Reinhardt, Hans-Wolf: Zeitstandzugfestigkeit von hochfestem Beton. beton 7+8/2004, S. 360 f
